首先是蓝桥杯的注意事项:
比赛前试好鼠标、键盘等设备,有问题要举手告诉监考老师
- 先想清楚思路怎么做再写代码,防止题目读假了。
- 请将题目通读完以后,再开始深入思考开始写你认为最容易的一道题。
- 为了方便,可以使用万能头文件 **#include **
- 一维
int型数组记最大可以开到 1e7 。 - C++ 一秒最多 5e8 次,建议记成 1e8 — 1e9,java py?
如果不会做了想暴力枚举的话,每题1s的限时,所以暴力枚举两个for嵌套,每个for最多可以运行10000次,三个for嵌套,每个for最多可以运行464次,大家做题的时候根据题目给的数据范围,可以估算一下暴力的话会不会超时。
int型变量最大记为 2e9 ,long long最大记为 1e18 (其实是9e18,主要记数量级),OI 赛制 不开long long见祖宗!- 输入输出建议直接使用
scanf和printf,或者ios加速后的cin和cout,但切记使用加速命令后cincout不要同时和scanf和printf一起使用。
直接放入
main() 函数开头即可。
- 输出的时候如果两个数字间有空格的话记得输出需要
printf("%d %d\n", a, b);(往期很多同学都会犯) - 大家如果平时不常用 debug 功能的话,可以去在关键处使用 printf 大法 去打印出关键变量(或者数组中的元素),思考一下写的代码和思路的结果是否相同。
- 题目的样例给的很少,可以自己去造几组数据进行测试(最好造边界、极端情况 ),考虑有没有负值、有没有特殊样例、有没有可能爆变量的最大值。
- 代码全都写进主函数有点难以调试,可以去 分块写 函数,哪里错了看哪里
- 最好熟悉使用一下 stl 的数据结构 string , map, set,queue, stack, priority_queue, vector等;同时最好也熟悉 stl 里的函数
尽管可以直接现查赛时提供的 帮助手册 ,但还是建议去用一用熟悉一下。
upper_bound() \ lower_bound()
find()
count()
substr()
sort()
reverse()
unique()
stoi(s)
atoi(s)
to_string()
等等...推荐个STL的网站:https://wyqz.top/p/870124582.html 比较好看~
- 基于 OI 赛制,可以先想暴力,再去想算法去优化时间/空间。
- 暴力即 枚举所有可能的答案,选最优的,也就是题目问什么就去枚举什么。
- 如果可以的话,直接模拟题目陈述的步骤即可。
- 对于 暴力 的方法,基本有以下几种:
- for循环直接枚举 数组\或者答案,(如果是答案的话立即想一下是否可以二分答案)
- 枚举排列组合的方案:dfs 飞机降落
- 想要找规律,可以直接写程序去找,而不是脑子硬想。
- 打表:可以在本地一直跑,跑出答案直接写到数组里,交程序时候直接读出数组中计算好的答案即可。
- 图论中暴力即 DFS、BFS 遍历所有点,最好去背背板子。
- 根据数据范围 反推 算法时间复杂度

二分
首先,二分查找的模板在此
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 100010; //根据题目中n的范围来确定数组应该开多大, 开的范围必须比n要大一点
int n, q; //n个数, q次询问
int arr[N]; //array
//第一个二分查找找的是: 被询问数的第一次出现的位置(下标)
int binary_search1(int arr[], int len, int x) {
int l = -1, r = len;
while(l + 1 < r) // l + 1 != r
{
int mid = (l + r) / 2;
if(arr[mid] < x) {
l = mid;
}
else r = mid;
}
if(arr[r] == x) return r;
else return -1; //找不到就返回-1
}
//第二个二分查找找的是: 被询问数的最后一次出现的位置(下标)
int binary_search2(int arr[], int len, int x) {
int l = -1, r = len;
while(l + 1 < r) {
int mid = (l + r) / 2;
if(arr[mid] <= x) {
l = mid;
}
else r = mid;
}
if(arr[l] == x) return l;
else return -1; //找不到就返回-1
}
int main() {
scanf("%d %d", &n, &q);
for(int i = 0; i < n; i ++) {
scanf("%d", &arr[i]);
}
while(q --) {
int x;
scanf("%d", &x);
int res1 = binary_search1(arr, n, x);
if(res1 == -1) {
printf("-1 -1\n");
continue;
}
int res2 = binary_search2(arr, n, x);
printf("%d %d\n", res1, res2);
}
return 0;
}关于二分需要注意的点:
- 数组大小要开的大一点,比如题干给 $n \le 10000$ ,咱们最好开 $10010$ 大的数组,防止越界。
- 注意二分 $l, r$ 的取值,如果数组从下标为 $1$ 处开始存,则 $l = 0, r = n + 1$ ;如果从下标为 $0$ 处开始存,则 $l = -1, r = n$ 即可。
- 要清楚边界线,以及怎么去划定自己需要的范围。
当取的值大过一个分界线之后,无论取哪个值都不可以满足条件。
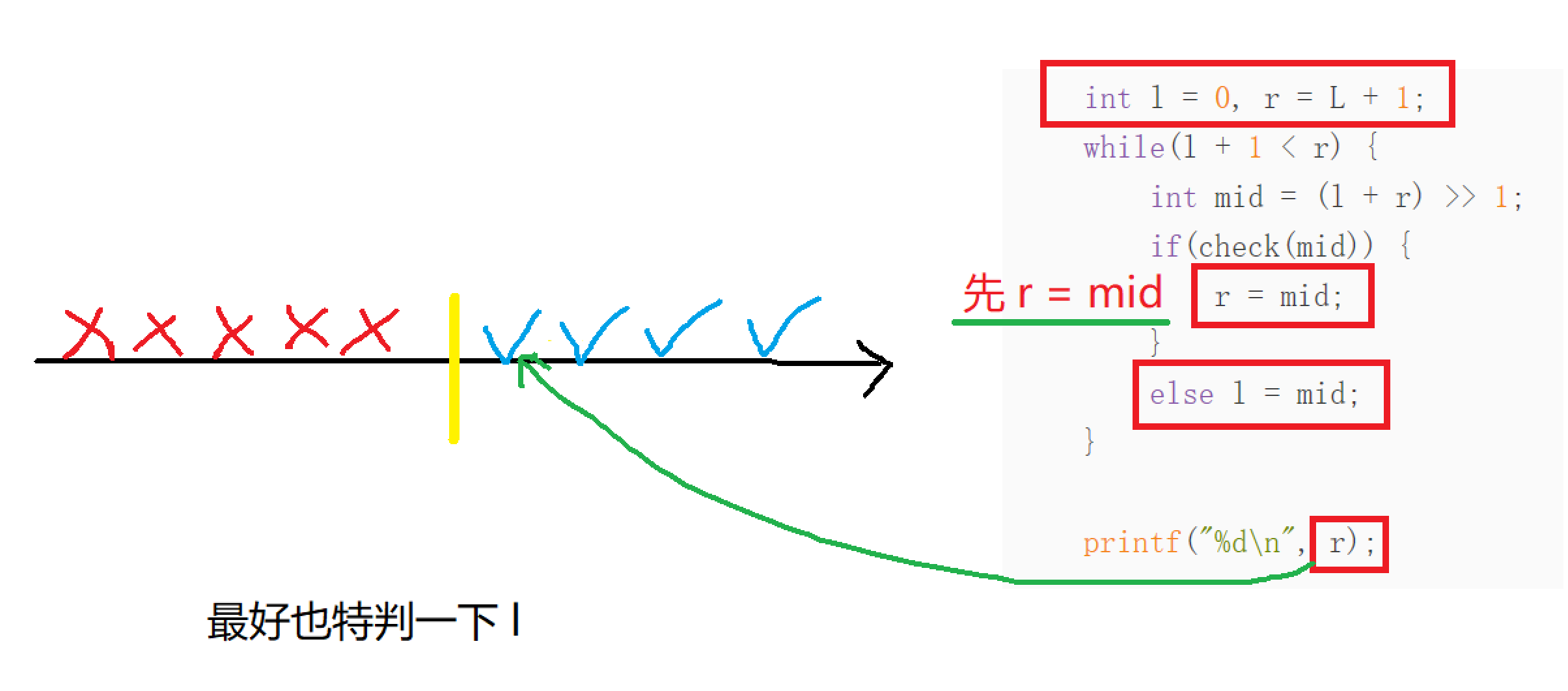
当取的值小过一个分界线之后,无论取哪个值都不可以满足条件。

相关视频(简介里有视频讲义和题目)
二分查找 | 妈妈再也不怕我写错二分啦 | 五点七边二分视频补充_哔哩哔哩_bilibili
二分习题课 | 手把手教你二分答案! | 超级细不听血亏_哔哩哔哩_bilibili
二分习题课补充 | P2853路标设置_哔哩哔哩_bilibili (第二种二分)
精讲浮点数二分 | 另一种二分应用场景_哔哩哔哩_bilibili
前缀和 和 差分
前缀和是指某序列的前 $n$ 项和,可以把它理解为数学上的数列的前 $n$ 项和,而差分可以看成前缀和的逆运算。合理的使用前缀和与差分,可以将某些复杂的问题简单化。


双指针
核心思想:优化暴力 (一般都是把暴力的 $O(n ^2)$ 优化到 $O(n)$ ),维护一些具有单调性、可快速删减的区间信息。

注意:
- 要保证两个指针的单调性,即不能回头走 (如果向前走就一直向前走)。
- 如果无序的话,可能需要先排个序。
- 用到的基本是 快慢指针 和 对撞指针。
相关视频(简介里有视频讲义和题目)
双指针 + 前缀和知识点课 | 一节课让你搞懂双指针思想!_哔哩哔哩_bilibili
双指针习题课 | 不听血亏 | 全新的思维方式_哔哩哔哩_bilibili
DFS – 不撞南墙不回头
void dfs()//参数用来表示状态
{
if(到达终点状态)
{
...//根据题意添加
return;
}
if(越界或者是不合法状态)
...//根据题意添加
return;
if(特殊状态)//剪枝
...//根据题意添加
return ;
for(扩展方式)
{
if(扩展方式所达到状态合法)
{
修改操作;//根据题意来添加
标记;
dfs();
(还原标记);
//是否还原标记根据题意
//如果加上(还原标记)就是 回溯法
}
}
} 注意:
- 注意枚举的顺序,要做到对每个点都依次枚举到。
- 注意输出方案时 $return$ 的位置。
- 要从数据存入的第一个点开始依次搜(比如数组从 $1$ 开始存,那么 $dfs(1)$ )。
- 迷宫问题的方向数组别写错
- $dfs$ 前可以预处理
相关视频(简介里有视频讲义和题目)
递推与递归 + DFS | 手把手带你画出递归搜索树_哔哩哔哩_bilibili
DFS正确入门方式 | DFS + 递归与递推习题课(上) | 一节课教你爆搜!_哔哩哔哩_bilibili
DFS正确入门方式 | DFS + 递归与递推习题课(下) | 一节课教你爆搜!_哔哩哔哩_bilibili
BFS – 一石惊起千层浪,泛起层层涟漪~
#define pair<int, int> PII
void bfs()
{
queue<PII> q; //一般用stl库中的queue来实现队列比较方便
q.push(起点S); //将初始状态入队
标记初始状态已入队。
while(!q.empty())//队列不为空就执行入队出队操作
{
top = q.front();//取出队头
q.pop();//队首出队
for (枚举所有可扩展的状态)
{
if (check())//状态合法
{
q.push(temp);//状态入队
标记成已入队。
}
}
}BFS可用于解决两类问题:
1.从A出发是否存在到达B的路径;DFS也可求
2.从A出发到达B的最短路径;数据小20以内的话, DFS也不是不可以 题眼
整体思路
其思路为从图上一个节点出发,访问先访问其直接相连的子节点,若子节点不符合,再问其子节点的子节点,按级别顺序(一层一层)依次访问,直到访问到目标节点。
步骤
- 起始:将起点(源点,树的根节点)放入队列中
- 扩散:从队列中取出队头的结点,将它的相邻结点放入队列,不断重复这一步
- 终止:当队列为空时,说明我们遍历了所有的能到的结点,整个图能到的点都被搜索了一遍
相关视频(简介里有视频讲义和题目)
BFS知识点课 | 一节课带你搞懂BFS | 凭什么为什么你怎么知道要用队列?_哔哩哔哩_bilibili
BFS习题课(上) | 从此搞懂搜索题的套路! | 入门必看_哔哩哔哩_bilibili
BFS 习题课(下) | 带你深入浅出 BFS 专题! | 下一站, DP!_哔哩哔哩_bilibili
DP
动态规划思路: dfs暴力 –> 记忆化搜索 –> 递推
1dfs > 2记忆化搜索 > 3逆序递推 > 4顺序递推 > 5优化空间 !
写出递推公式的方法:
递推 的公式 = $dfs$ 向下 递归 的公式
递推 数组的初始值 = 递归 的边界
动态规划做题步骤
- 重述问题
- 找到最后一步
- 去掉最后一步,是否能划分出子问题
- 考虑边界
dp不会写可以直接写dfs 跑路(最好加个记忆化mem,能剪枝也可以剪枝)
相关视频(简介里有视频讲义和题目)
动态规划(dp)入门 | 这tm才是入门动态规划的正确方式! | dfs记忆化搜索 | 全体起立!!_哔哩哔哩_bilibili
DP之背包问题 | 01背包 + 完全背包 | 逐步推进,深入解析!_哔哩哔哩_bilibili
动态规划入门刷题课(上)| 新手必看必学 | dp四部曲_哔哩哔哩_bilibili
动态规划入门刷题课(下)| 新手入门动态规划必看!! | dp四步曲_哔哩哔哩_bilibili
图论板子
堆优化版dijkstra —— 模板题 AcWing 850. Dijkstra求最短路 II
时间复杂度 $O(mlogn)$ ,$n$ 表示点数, $m$ 表示边数。
typedef pair<int, int> PII;
int n; // 点的数量
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储所有点到1号点的距离
bool st[N]; // 存储每个点的最短距离是否已确定
// 求1号点到n号点的最短距离,如果不存在,则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1}); // first存储距离,second存储节点编号
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}floyd算法 —— 模板题 AcWing 854. Floyd求最短路
时间复杂度 $(O^3)$ , $n$ 表示点数。
初始化:
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
// 算法结束后,d[a][b]表示a到b的最短距离
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}Kruskal算法 —— 模板题 AcWing 859. Kruskal算法求**最小生成树 **
时间复杂度 $O(mlogm)$ ,$n$ 表示点数, $m$ 表示边数。
int n, m; // n是点数,m是边数
int p[N]; // 并查集的父节点数组
struct Edge // 存储边
{
int a, b, w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[M];
int find(int x) // 并查集核心操作
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal()
{
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
int res = 0, cnt = 0;
for (int i = 0; i < m; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b) // 如果两个连通块不连通,则将这两个连通块合并
{
p[a] = b;
res += w;
cnt ++ ;
}
}
if (cnt < n - 1) return INF;
return res;
}以下算法最好掌握一下。