本文最后更新于 309 天前,其中的信息可能已经有所发展或是发生改变。
算法概述
算法的5大特性
- 确定性:算法的每一步骤必须有明确的定义,无二义性。即在相同输入下,每次执行都应得到相同的结果。
- 能行性:算法的每一步都必须是可实现的,即在有限时间内能用有限资源完成。
- 输入:算法可以有零个或多个输入,输入是算法处理的初始数据。
- 输出:算法必须有一个或多个输出,输出是算法处理的结果。
- 有穷性/有限性:算法必须在执行有限步骤后终止,不能无限循环。
算法与计算过程的区别
计算过程可能无限执行(如操作系统),而算法必须是有穷的。
算法描述的主要语言
- 自然语言:直观但容易歧义。
- 伪代码:介于自然语言和编程语言之间,结构清晰,无语法限制。
- 流程图:图形化表示,直观展示控制流。
- 编程语言:直接实现,但需关注语法细节。
渐进表示
定义
- O(大O符号,上界):
f(n)=O(g(n)) 表示存在常数 c>0 和 n0,使得对所有 n≥n0,有 f(n)≤c⋅g(n)。- 表示算法的最坏情况时间复杂度。
- Ω(Omega,下界):
f(n)=Ω(g(n)) 表示存在常数 c>0 和 n0,使得对所有 n≥n0,有 f(n)≥c⋅g(n)。- 表示算法的最好情况时间复杂度。
- Θ(Theta,紧确界):
f(n)=Θ(g(n)) 当且仅当 f(n)=O(g(n)) 且 f(n)=Ω(g(n))。- 表示算法的平均情况时间复杂度。
多项式定理
若 f(n) 是 d 次多项式,则 f(n)=Θ(nd)。
常见的多项式/指数限界函数
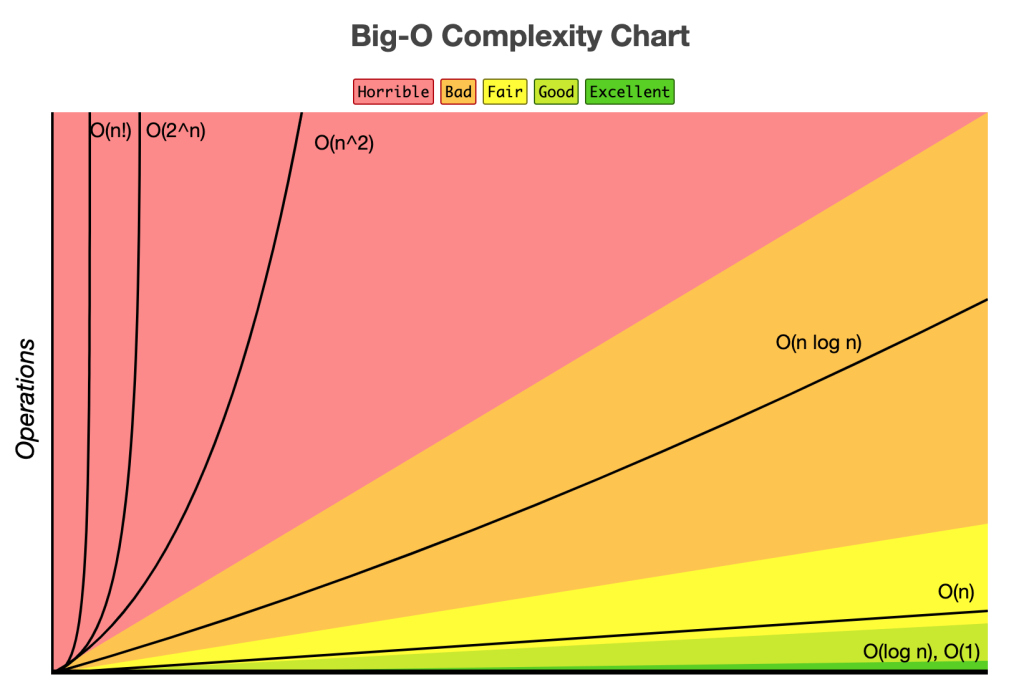
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)
渐进符号O运算性质
- 传递性:若 f(n)=O(g(n)) 且 g(n)=O(h(n)),则 f(n)=O(h(n))。
- 加法规则:O(f(n))+O(g(n))=O(max(f(n),g(n)))。
- 乘法规则:O(f(n))⋅O(g(n))=O(f(n)⋅g(n))。
重要例题
冒泡排序
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
return arr
# 示例
print(bubble_sort([64, 34, 25, 12, 22, 11, 90])) # 输出: [11, 12, 22, 25, 34, 64, 90]警察抓小偷
信息数字化。
竞赛预测
信息数字化。将逻辑问题转化为代码,遍历求解。
楼梯台阶问题
def climb_stairs(n):
if n <= 2:
return n
a, b = 1, 2
for _ in range(3, n+1):
a, b = b, a + b
return b
# 示例
print(climb_stairs(5)) # 输出: 8(5阶有8种走法)算法的基本工具
递归设计要点
- 基准情形:明确递归终止条件(如 n=0 或 n=1)。
- 递归调用:将问题分解为更小的同类子问题。
- 正确性证明:通常用数学归纳法验证。
循环与递归的比较
| 比较维度 | 循环(迭代) | 递归 |
|---|---|---|
| 程序可读性 | 通常更直观,适合线性逻辑(如遍历数组)。 | 更符合数学思维,适合分治、树/图遍历等问题,但嵌套过深时难理解。 |
| 代码量 | 通常较短,尤其是简单循环(如 for、while)。 | 可能更简洁(如阶乘、斐波那契数列),但需要额外递归终止条件。 |
| 时间效率 | 无函数调用开销,执行更快(适合大规模数据)。 | 每次递归调用需保存栈帧,函数调用开销大,可能更慢。 |
| 占用空间 | 仅需固定内存(如几个变量),空间复杂度通常为 O(1)。 | 需保存每一层调用的栈帧,空间复杂度取决于递归深度(如 O(n) 或 O(logn)),可能栈溢出。 |
| 适用范围 | 所有可迭代问题(如数组遍历、数值计算)。 | 适合分治(如归并排序)、回溯(如八皇后)、树/图遍历(如DFS)等递归定义的问题。 |
| 设计难度 | 较直观,适合顺序逻辑。 | 需找到子问题分解方式,设计递归终止条件,对思维抽象能力要求更高。 |
一般的,理论上,循环(迭代)都可以改写成递归,反之不然。
常用数据结构的比较
- 数组:随机访问快,插入/删除慢。
- 链表:插入/删除快,访问需遍历。
- 栈/队列:特定顺序操作(LIFO/FIFO)。
- 哈希表:快速查找,但需处理冲突。
重要例题
欧几里得算法
def gcd(a, b):
while b:
a, b = b, a % b
return a
# 示例
print(gcd(48, 18)) # 输出: 6Hanoi塔
def hanoi(n, source, target, auxiliary):
"""
汉诺塔递归解法
:param n: 盘子数量
:param source: 起始柱子(如 'A')
:param target: 目标柱子(如 'C')
:param auxiliary: 辅助柱子(如 'B')
"""
if n == 1:
# 基准情形:只有一个盘子时,直接移动到目标柱子
print(f"Move disk 1 from {source} to {target}")
else:
# 递归步骤:
# 1. 将前 n-1 个盘子从 source 移到 auxiliary(借助 target)
hanoi(n-1, source, auxiliary, target)
# 2. 将第 n 个盘子(最大的)从 source 移到 target
print(f"Move disk {n} from {source} to {target}")
# 3. 将前 n-1 个盘子从 auxiliary 移到 target(借助 source)
hanoi(n-1, auxiliary, target, source)
# 示例:移动 3 个盘子从 A 到 C,借助 B
hanoi(3, 'A', 'C', 'B')整数的划分
def integer_partition(n, m):
"""
计算将整数 n 划分为最大部分不超过 m 的划分数。
:param n: 待划分的整数。
:param m: 划分中允许的最大部分。
"""
if n == 0:
return 1 # 空划分算一种
if m == 1:
return 1 # 只能划分为 1+1+...+1
if n < m:
return integer_partition(n, n)
return integer_partition(n, m-1) + integer_partition(n-m, m)
# 示例:计算 n=5 的所有划分数
print(integer_partition(5, 5)) # 输出: 7n个自然数中r个数的组合
递归生成所有组合,避免重复。
杨辉三角形
递推关系:C(n,k)=C(n−1,k−1)+C(n−1,k)。
递推关系求解方程
如斐波那契数列:可通过特征方程求通项公式。
迭代算法
迭代算法的设计步骤(3步)
- 初始化:设定初始状态(如变量初值)。
- 迭代过程:通过循环逐步更新状态。
- 终止条件:达到目标时退出循环。
递推法vs倒推法
- 递推法:从已知条件逐步推导到目标(如斐波那契数列)。
- 倒推法:从目标反向推导初始条件(如猴子吃桃问题)。
重要例题
兔子繁衍问题
def fibonacci(n):
a, b = 0, 1
for _ in range(n):
a, b = b, a + b
return a
# 示例
print(fibonacci(6)) # 输出: 8(第6个月有8对兔子)猴子吃桃问题
def peach_count(days):
peaches = 1 # 最后一天剩1个
for _ in range(days-1):
peaches = (peaches + 1) * 2
return peaches
# 示例
print(peach_count(5)) # 输出: 46(第1天有46个桃子)杨辉三角形
递推关系:C(n,k)=C(n−1,k−1)+C(n−1,k)。
穿越沙漠问题(重点在于如何理解其思想)
核心思想:分段设立补给站,逆向计算资源消耗。
牛顿迭代法
求方程根:xn+1=xn−f(xn)/f′(xn)。
蛮力法
重要例题
百钱百鸡问题
def hundred_chickens():
for x in range(0, 21): # 公鸡最多20只
for y in range(0, 34): # 母鸡最多33只
z = 100 - x - y
if 5*x + 3*y + z/3 == 100:
print(f"公鸡: {x}, 母鸡: {y}, 小鸡: {z}")
# 示例
hundred_chickens() # 输出所有解解数字迷(ABCAB X A = DDDDDD)
def solve_abcab():
for a in range(1, 10):
for b in range(10):
for c in range(10):
abcab = 10000*a + 1000*b + 100*c + 10*a + b
d = abcab * a
if len(str(d)) == 6 and len(set(str(d))) == 1:
print(f"ABCAB = {abcab}, A = {a}, D = {d}")
# 示例
solve_abcab() # 输出: ABCAB = 37037, A = 3, D = 111111狱吏问题(蛮力->数学技巧->深入挖掘数学规律)
def prison_doors(n):
doors = [False] * n # False表示门关闭
for i in range(1, n+1):
for j in range(i-1, n, i):
doors[j] = not doors[j]
return [i+1 for i, door in enumerate(doors) if door]
# 示例
print(prison_doors(10)) # 输出: [1, 4, 9](完全平方数编号的门开着)