本文最后更新于 242 天前,其中的信息可能已经有所发展或是发生改变。
见到很有意思的问题 : 以往见过许多教材,对动态规划(DP)的引入属于“奉天承运,皇帝诏曰”式:不给出一点引入,见面即拿出一大堆公式吓人;学生则死啃书本,然后突然顿悟。针对入门者的教材不应该是这样的。(看到一位知乎的大佬说的, 深有感悟~)
动态规划 就是 : 给定一个问题,我们把它拆成一个个子问题,直到子问题可以直接解决。然后把子问题的答案保存起来,以减少重复计算。再根据子问题答案反推,得出原问题解的一种方法.
那么我们今天就来带给大家 新手入门动态规划的正确方法!
记忆化搜索 = 暴力dfs + 记录答案
动态规划入门思路: dfs暴力 — 记忆化搜索 — 递推
1dfs > 2记忆化搜索 > 3逆序递推 > 4顺序递推 > 5优化空间 !
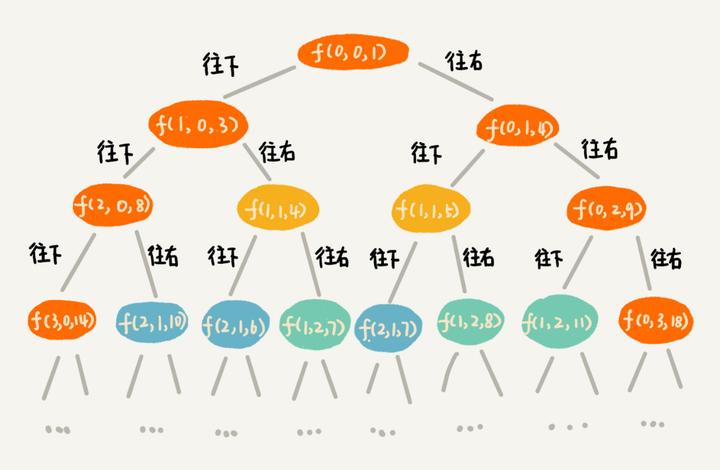
递归的过程:
“递” 的过程是: 分解子问题的过程;
“归” 的过程才是: 产生答案的过程;
“递” — 自顶向下, “归” — 自底向上 , 其中 “底” 是 递归搜索树 的底
写出递推公式的方法:
递推 的公式 = dfs 向下 递归 的公式
递推 数组的初始值 = 递归 的边界
例题
acwing821.跳台阶 \或者\ P1255. 数楼梯
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
int n;
int f[N];
int main()
{
f[1] = 1, f[2] = 2;
cin >> n;
int newf = 0, tmp1 = 1, tmp2 = 2;
for(int i = 3; i <= n; i++)
{
newf = tmp1 + tmp2;
tmp1 = tmp2;
tmp2 = newf;
}
cout << newf << endl;
tmp1 = 1, tmp2 = 2;
for(int i = 3; i <= n; i++)
{
tmp2 = tmp1 + tmp2;
tmp1 = tmp2 - tmp1;
}
cout << tmp2 << endl;
for (int i = 3; i <= n; i++)
{
f[i] = f[i - 1] + f[i - 2];
}
cout << f[n] << endl;
return 0;
}acw1049. 大盗阿福 \或者\ lc198. 打家劫舍
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, T;
int home[N];
int men[N];
int f[N];
int dfs(int x)
{
if (men[x])
return men[x];
int sum = 0;
if (x > n)
sum = 0;
else
sum = max(dfs(x + 1), dfs(x + 2) + home[x]);
men[x] = sum;
return sum;
}
int main()
{
cin >> T;
while (T--)
{
memset(men, 0, sizeof men);
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> home[i];
}
// int res = dfs(1);
// cout << res << endl;
// for (int i = n; i >= 1; i--)
// {
// f[i] = max(f[i+1],f[i+2]+home[i]);
// }
// cout << f[1] << endl;
// for (int i = 1; i <= n; i++)
// {
// f[i+2] = max(f[i+1],f[i]+home[i]);
// }
// cout << f[n+2] << endl;
int newf = 0, tmp1 = 0, tmp2 = 0;
for (int i = 1; i <= n; i++)
{
newf = max(tmp1, tmp2 + home[i]);
tmp2 = tmp1;
tmp1 = newf;
}
cout << newf << endl;
}
return 0;
}P1216 数字三角形
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n;
int g[N][N];
int mem[N][N];
int f[N][N];
int h[N];
int dfs(int x, int y)
{
if (mem[x][y])
return mem[x][y];
// if (x>n||y>n) return 0;
// // 求 最优子问题 dfs(x)=max(dfs(x+1),dfs(x+2))
// // 求 子问题的和 dfs(x)=dfs(x+1)+dfs(x+2)
// else return max(dfs(x+1,y),dfs(x+1,y+1))+g[x][y];
int sum = 0;
if (x > n || y > n)
sum = 0;
else
sum = max(dfs(x + 1, y), dfs(x + 1, y + 1)) + g[x][y];
mem[x][y] = sum;
return sum;
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
cin >> g[i][j];
// int res = dfs(1, 1);
// cout << res << endl;
// for (int i = n; i >= 1; i -- )
// for (int j = 1; j <= i; j ++ )
// f[i][j] = max(f[i+1][j],f[i+1][j+1])+g[i][j];
// cout << f[1][1] << endl;
// for(int i=1;i<=n;i++)
// for(int j=1;j<=i;j++)
// f[i][j]=max(f[i-1][j],f[i-1][j-1])+g[i][j];
// int res=0;
// for(int i=1;i<=n;i++)
// res=max(res,f[n][i]);
// cout<<res<<endl;
// for (int i = n; i >= 1; i--)
// for (int j = 1; j <= i; j++)
// h[j] = max(h[j], h[j + 1]) + g[i][j];
// cout << h[1] << endl;
for (int i = n; i >= 1; i--)
for (int j = 1; j <= i; j++)
g[i][j] = max(g[i+1][j],g[i+1][j+1]) + g[i][j];
cout << g[1][1] << endl;
return 0;
}acwing2. 01背包问题
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int res = 0;
void dfs(int x, int sumV, int sumW)
{
if (x > n)
{
if (sumV <= m && sumW >= res)
{
res = sumW;
}
return;
}
// 不选
dfs(x + 1, sumV, sumW);
// 选
if (sumV + v[x] <= m)
dfs(x + 1, sumV + v[x], sumW + w[x]);
}
int main()
{
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
{
scanf("%d %d", &v[i], &w[i]);
}
dfs(1, 0, 0);
printf("%d\n", res);
return 0;
}#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int res = 0;
int mem[N][N];
int f[N][N];
int g[N];
int dfs(int x, int spV)
{
if (mem[x][spV])
{
return mem[x][spV];
}
int sum = 0;
if (x > n)
{
sum = 0;
}
else if (spV < v[x])
{
sum = dfs(x + 1, spV);
}
else if (spV >= v[x])
{
sum = max(dfs(x + 1, spV), dfs(x + 1, spV - v[x]) + w[x]);
}
mem[x][spV] = sum;
return sum;
}
int main()
{
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
{
scanf("%d %d", &v[i], &w[i]);
}
// int res = dfs(1, m);
// printf("%d\n", res);
// for (int i = n; i >= 1; i--)
// {
// for (int j = 0; j <= m; j++)
// {
// if (j < v[i])
// {
// f[i][j] = f[i + 1][j];
// }
// else if (j >= v[i])
// {
// f[i][j] = max(f[i + 1][j], f[i + 1][j - v[i]] + w[i]);
// }
// }
// }
// cout<<f[1][m]<<endl;
for (int i = 1; i <= n; i++)
{
for (int j = 0; j <= m; j++)
{
if (j < v[i])
{
f[i][j] = f[i - 1][j];
}
else if (j >= v[i])
{
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
}
}
}
cout << f[n][m] << endl;
return 0;
}习题
P1044 栈
P1164 小A点菜
P1130 红牌
…
用以上思路, 找动态规划的简单题慢慢去写熟练, 熟练之后直接写出递推式即可~