算法主要原理
算法流程如下:
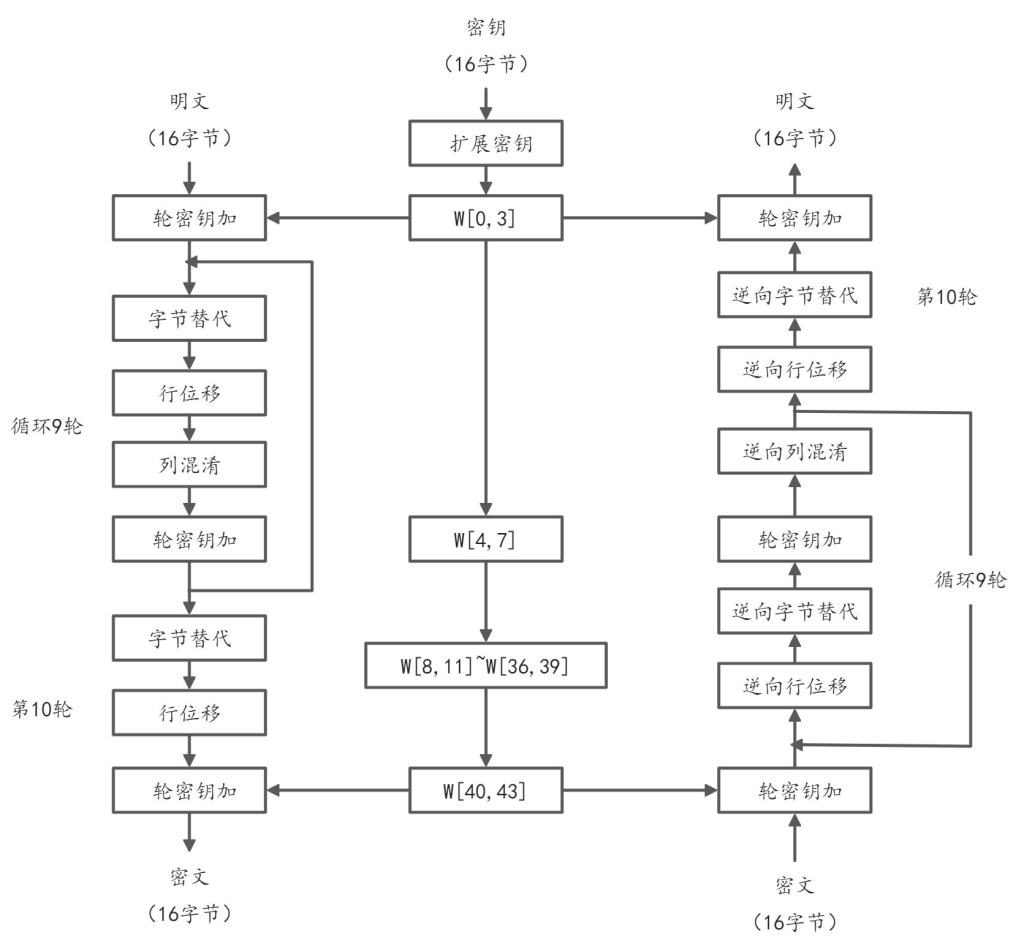
算法步骤
AES算法是一种对称分组密码算法,采用代换-置换网络(SPN)结构,通过多轮迭代的加密过程对数据进行混淆和扩散,确保其安全性。该算法将明文分成固定长度的128位数据块(实际上分组长度也有128位、192位或256位三种选择),并支持128位、192位或256位的密钥,分别对应10轮、12轮或14轮的加密轮次。每一轮加密过程包括四个核心操作:字节代换、行移位、列混淆和轮密钥加,其中最后一轮省略列混淆步骤。通过密钥扩展算法,初始密钥被扩展为多组轮密钥,供每一轮加密使用。AES算法的安全性依赖于其非线性的S盒变换、扩散层操作以及密钥的复杂性,使其能够有效抵抗线性攻击和差分攻击,成为当前最广泛使用的对称加密标准之一。
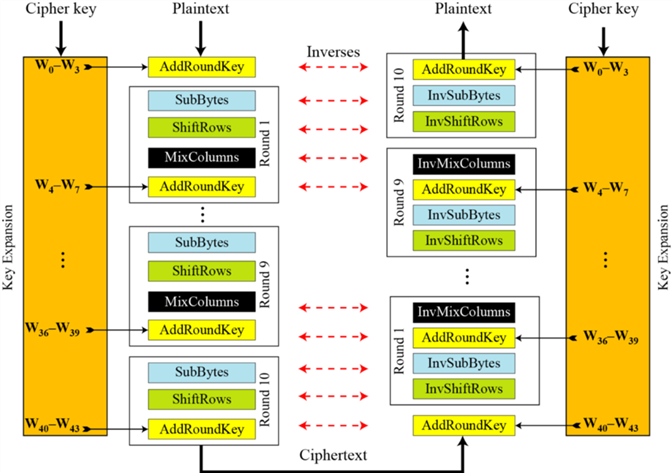
1.字节代换
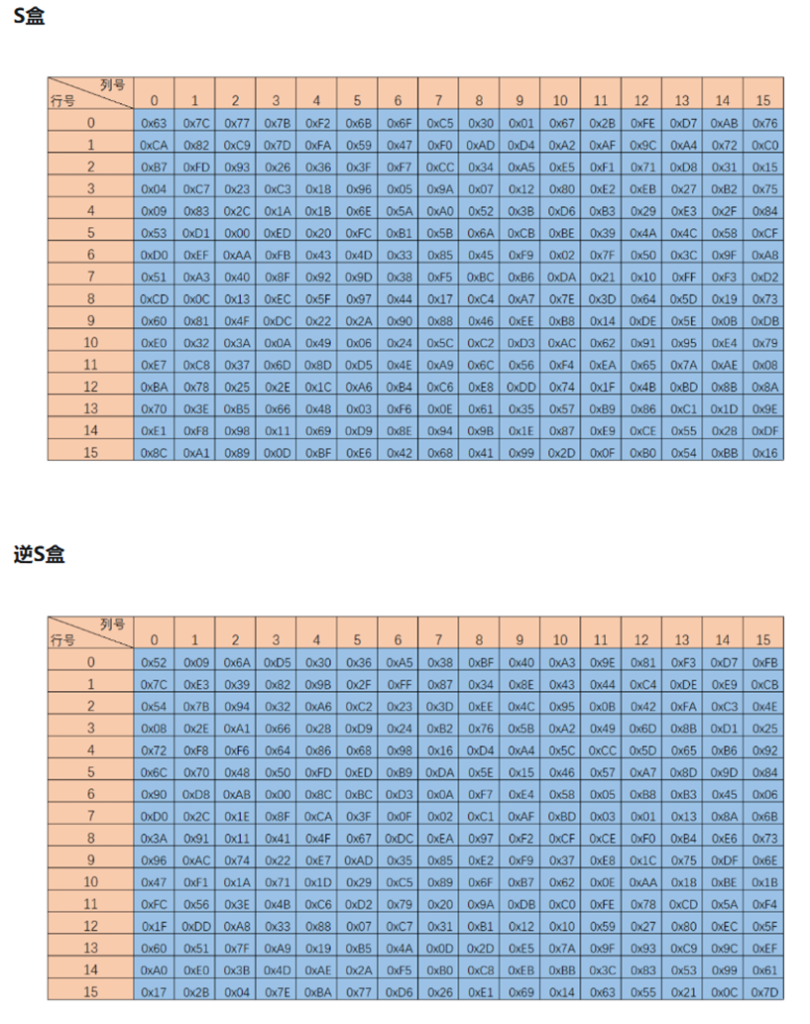
字节代换是AES加密的核心非线性变换,它通过一个被称为S盒的查找表对状态矩阵中的每个字节进行独立替换。其中,S盒是经过精心设计的,它基于有限域GF(2⁸)上的乘法逆运算,再加上一个仿射变换,使得输出与输入之间不存在明显的数学关系。具体来说,每个字节先被看作GF(2⁸)中的元素,计算其乘法逆元(0x00映射到自身),然后经过一个固定的仿射变换。这种设计让S盒具备极强的非线性特性,有效抵抗线性密码分析。而解密过程则使用逆S盒进行反向替换,但这两个S盒并不是简单的互逆关系,而是各自独立构造的。
2.行移位
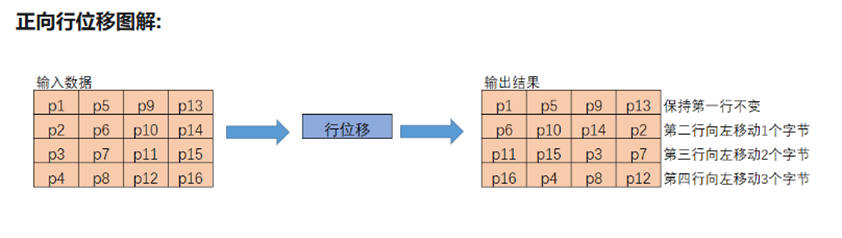
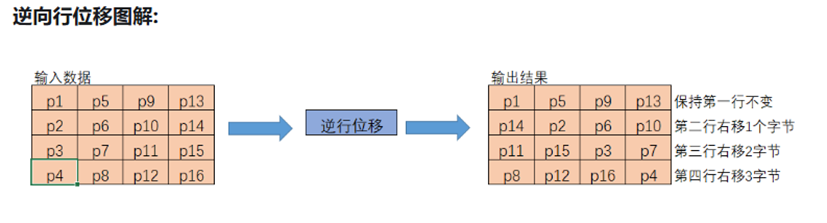
行移位步骤是对状态矩阵的行进行循环移位操作。具体来说,状态矩阵是一个4行4列的字节数组。第一行保持不变,第二行循环左移1个字节,第三行循环左移2个字节,第四行循环左移3个字节。这个操作使得原本在同一列中的字节被分散到不同列中。在解密时,需要进行相反方向的循环右移操作。行移位的目的是实现字节在状态矩阵中的扩散,使得后续的列混淆操作能更有效地传播变化。
3.列混淆
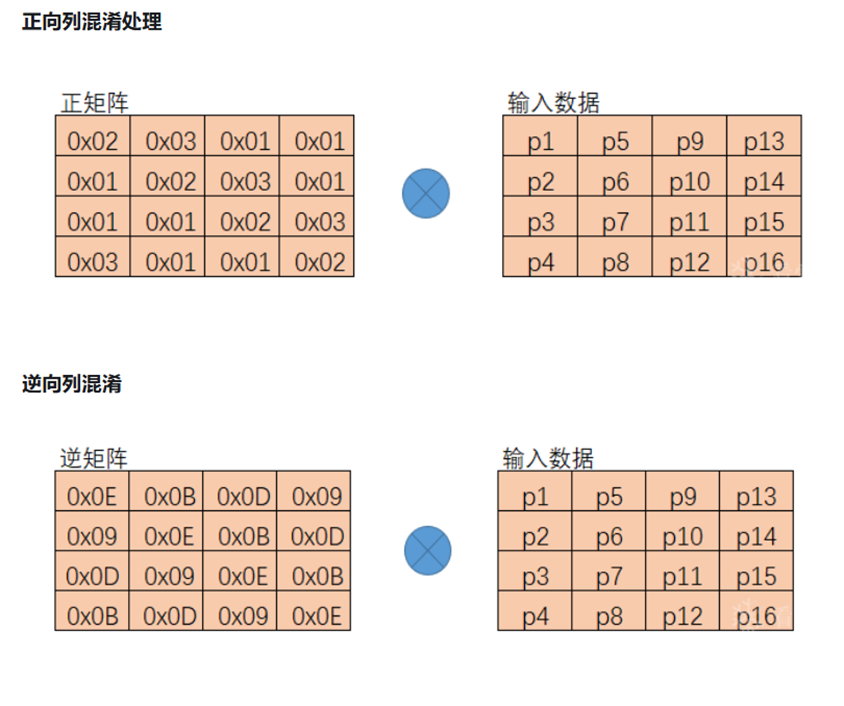
列混淆步骤对状态矩阵的每一列进行线性变换。该操作将每一列视为GF(2^8)上的多项式,与固定多项式进行有限域上的乘法。这个运算可以表示为矩阵乘法,其中每个字节的变换都是与固定系数的乘法和异或组合。
在实际实现中,这个步骤可以使用xtime进行化简。xtime定义为这样的一个函数,其输入是一个 8 位字节(即 GF(2⁸) 的元素),输出是该字节与 {02}(即多项式 x)相乘的结果,并在必要时进行模 x⁸ + x⁴ + x³ + x + 1(AES 使用的不可约多项式)的约简,也即异或0x1B。
在解密时,只需要变换固定系数矩阵即可。值得注意的是,最后一轮加密不包含列混淆操作。这个步骤增强了AES的扩散特性,使得单个字节的变化会影响整个列。
4.轮密钥加
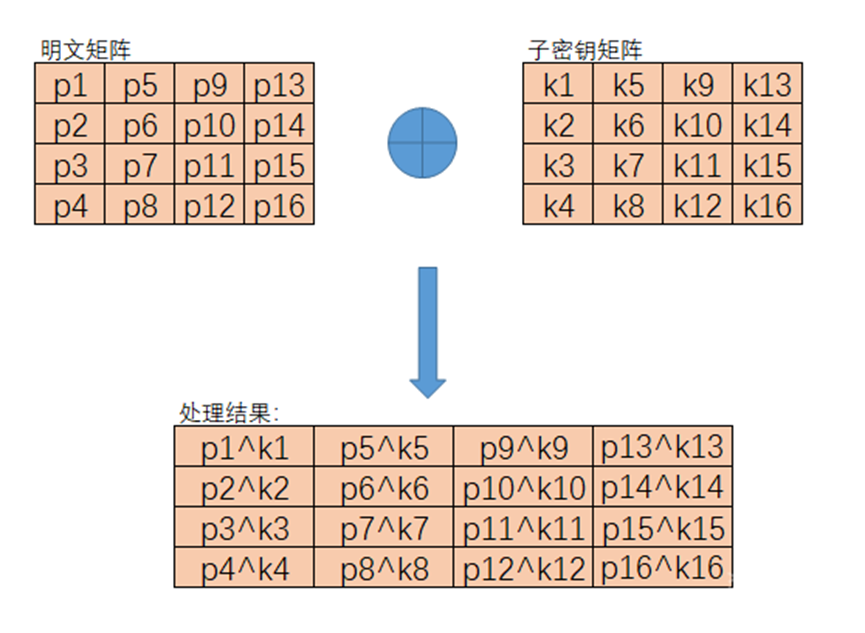
轮密钥加步骤将当前轮的扩展密钥与状态矩阵进行简单的按位异或操作。每一轮都使用不同的轮密钥,这些密钥是通过密钥扩展算法从初始密钥派生出来的。这个操作是AES中唯一直接使用密钥的步骤。由于异或操作的可逆性,解密时只需使用相同的轮密钥再次异或即可恢复原始数据。这个步骤为算法提供了基于密钥的安全性。
5.密钥扩展算法
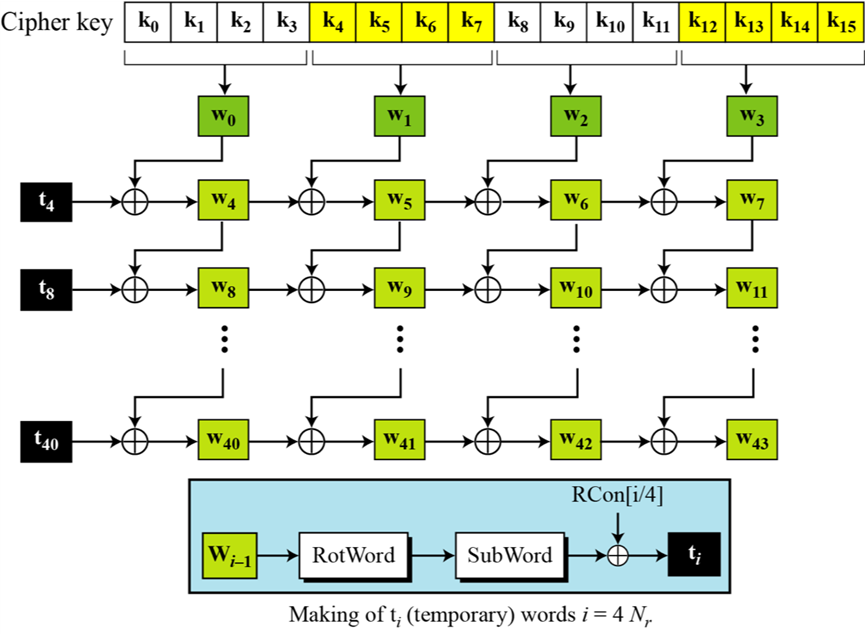
密钥扩展算法负责从初始密钥生成各轮所需的轮密钥。对于128位密钥,需要生成10个轮密钥(共44个32位字)。算法首先将初始密钥分成4个字(w[0]-w[3]),然后递归生成后续的字。我们这里只讨论128位密钥的扩展,其他位数的扩展步骤大致相同。
对于非4k个字,计算方式为前一个字w[i-1]与w[i-4]的简单异或(XOR)。每第4k个字(如w[4],w[8]等)需要特殊处理,计算方式为先对前一个字w[i-1]进行字节代换、循环移位,再与w[i-4]、轮常数异或。轮常数是一个与轮次相关的固定值,用于打破对称性。对于192位和256位密钥,扩展过程类似但细节略有不同。这个算法确保每个轮密钥都与前一个不同,且整个密钥调度具有足够的随机性。
6.DES与AES的对比
DES和AES在结构设计上采用了不同的密码学架构,体现了对称加密算法演进的思路。DES基于Feistel网络结构,这种结构将输入分组分为左右两部分,每轮只对其中一半进行加密变换,再通过交换左右部分实现数据混淆。Feistel结构的特点是加密解密过程对称,只需调整子密钥顺序即可实现逆向运算,这使得硬件实现相对简单。然而DES的56位密钥长度在计算能力提升后显得不足,且固定的S盒设计存在潜在的分析风险。
AES则采用了更为现代的SPN(Substitution-Permutation Network)结构,这种结构通过多轮重复的代换和置换操作实现数据加密。与Feistel网络不同,SPN结构在每一轮都对整个数据块进行完整的非线性变换和线性扩散。具体来说,AES的每轮加密都包含字节代换、行移位、列混淆和轮密钥加四个步骤,其中前三步分别实现非线性代换和线性扩散,最后一步引入密钥相关变换。这种设计使得AES在相同轮数下能实现更强的混淆和扩散效果。
从安全性角度来看,AES的SPN结构具有明显优势。其更大的分组长度(128位起)和可变的密钥长度(128/192/256位)能更好抵抗穷举攻击。每一轮对整个数据块的处理方式使得差分和线性分析更加困难,而DES的Feistel结构由于每轮只处理半块数据,需要更多轮数才能达到相似的混淆效果。此外,AES的S盒设计基于严密的数学理论,相比DES的固定S盒具有更强的抗分析能力。
在性能表现上,AES的SPN结构更适合现代计算环境。其算法设计充分考虑了软硬件实现的效率,在各类平台上都能展现出优异的性能。而DES由于其初始设计年代较早,在软件实现效率上相对较低,特别是在处理大数据量时更为明显。AES的轮数可以根据密钥长度灵活调整(10/12/14轮),在安全性和效率之间取得了更好的平衡。
NIST提出AES标准的主要原因在于DES已不能满足现代安全需求。随着计算能力的提升,DES的56位密钥面临被暴力破解的风险。1997年DES挑战赛被成功攻破,加速了新标准的制定进程。AES的选拔过程公开透明,最终Rijndael算法因其在安全性、性能和实现灵活性上的综合优势胜出。相比DES,AES提供了更高的安全强度、更优的执行效率以及更好的算法透明度,这些特点使其成为21世纪最重要的对称加密标准。
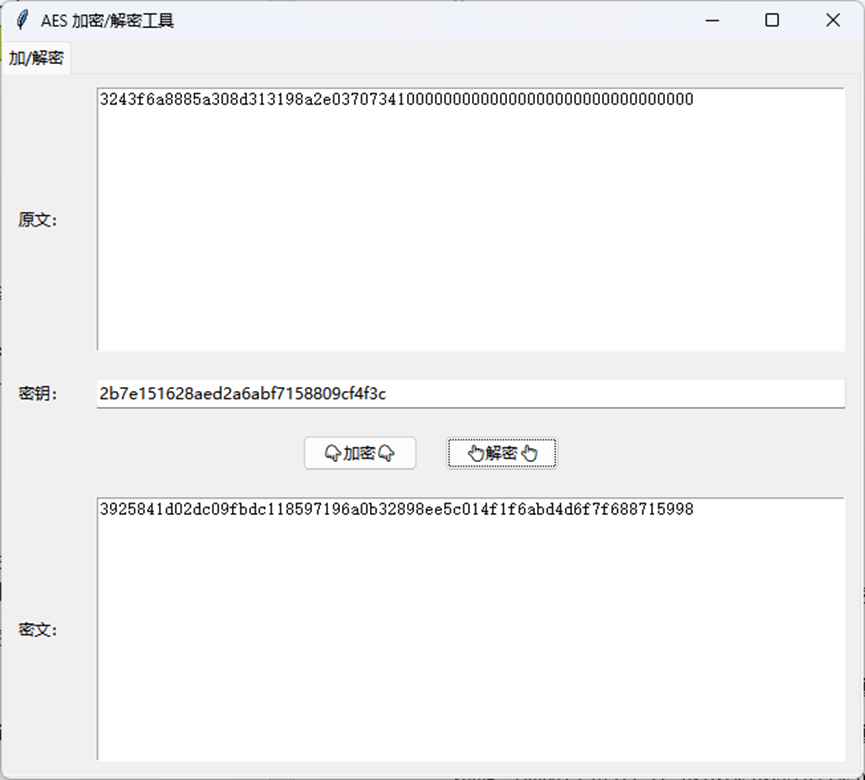
程序运行截图
参考代码
aes.py
# AES 128 bit encryption and decryption
# 128 bit 密钥 == 16 bytes == 32位十六进制
# 192 bit 密钥 == 24 bytes == 48位十六进制
# 256 bit 密钥 == 32 bytes == 64位十六进制
Sbox = (
0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)
InvSbox = (
0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D,
)
# xtime函数,用于有限域上的乘法运算
# 如果a的最高位为1,则左移1位后与0x1B异或,否则直接左移1位
# 0x1B 是 0001 1011 的十六进制表示,
# 0xFF 是 1111 1111 的十六进制表示,& 0xFF 运算只保留最低8位,其余位为0
# 0x80 是 1000 0000 的十六进制表示,& 0x80 运算只保留最高位,其余位为0
xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)
# Rcon常量,用于密钥扩展
Rcon = (
0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,
0x80, 0x1B, 0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A,
0x2F, 0x5E, 0xBC, 0x63, 0xC6, 0x97, 0x35, 0x6A,
0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5, 0x91, 0x39,
)
def text2matrix(text):
# 将文本转换为矩阵
matrix = []
for i in range(16):
# 每次取出8位(1字节)
byte = (text >> (8 * (15 - i))) & 0xFF
if i % 4 == 0:
# 每4个字节开始一个新行
matrix.append([byte])
else:
# 将字节添加到当前行
matrix[int(i / 4)].append(byte)
return matrix
def matrix2text(matrix):
# 将矩阵转换为文本
text = 0
for i in range(4):
for j in range(4):
# 将每个字节移动到正确的位置并组合
text |= (matrix[i][j] << (120 - 8 * (4 * i + j)))
return text
class AES:
def __init__(self, master_key):
# 初始化密钥
self.change_key(master_key)
def change_key(self, master_key):
# 更改密钥
self.round_keys = text2matrix(master_key)
for i in range(4, 4 * 11):
self.round_keys.append([])
# 4的倍数
if i % 4 == 0:
# 列i-4 异或 列i-1 异或 轮常量Rcon[int(i / 4)]
# 旋转字节
# 第一个字节--》取原来的第二个字节,然后代换
byte = self.round_keys[i - 4][0] \
^ Sbox[self.round_keys[i - 1][1]] \
^ Rcon[int(i / 4)]
self.round_keys[i].append(byte)
# 其他三个字节
# 原字节都向后移一位
for j in range(1, 4):
byte = self.round_keys[i - 4][j] \
^ Sbox[self.round_keys[i - 1][(j + 1) % 4]]
self.round_keys[i].append(byte)
# 不是4的倍数
else:
# 列i-4 异或 列i-1
for j in range(4):
byte = self.round_keys[i - 4][j] \
^ self.round_keys[i - 1][j]
self.round_keys[i].append(byte)
# print(self.round_keys)
def encrypt(self, plaintext):
# 加密函数
self.plain_state = text2matrix(plaintext)
self.__add_round_key(self.plain_state, self.round_keys[:4])
for i in range(1, 10):
self.__round_encrypt(self.plain_state, self.round_keys[4 * i : 4 * (i + 1)])
self.__sub_bytes(self.plain_state)
self.__shift_rows(self.plain_state)
self.__add_round_key(self.plain_state, self.round_keys[40:])
return matrix2text(self.plain_state)
def decrypt(self, ciphertext):
# 解密函数
self.cipher_state = text2matrix(ciphertext)
self.__add_round_key(self.cipher_state, self.round_keys[40:])
self.__inv_shift_rows(self.cipher_state)
self.__inv_sub_bytes(self.cipher_state)
for i in range(9, 0, -1):
self.__round_decrypt(self.cipher_state, self.round_keys[4 * i : 4 * (i + 1)])
self.__add_round_key(self.cipher_state, self.round_keys[:4])
return matrix2text(self.cipher_state)
def __add_round_key(self, s, k):
# 轮密钥加
for i in range(4):
for j in range(4):
s[i][j] ^= k[i][j]
def __round_encrypt(self, state_matrix, key_matrix):
# 轮加密
self.__sub_bytes(state_matrix)
self.__shift_rows(state_matrix)
self.__mix_columns(state_matrix)
self.__add_round_key(state_matrix, key_matrix)
def __round_decrypt(self, state_matrix, key_matrix):
# 轮解密
self.__add_round_key(state_matrix, key_matrix)
self.__inv_mix_columns(state_matrix)
self.__inv_shift_rows(state_matrix)
self.__inv_sub_bytes(state_matrix)
def __sub_bytes(self, s):
# 字节代换
for i in range(4):
for j in range(4):
s[i][j] = Sbox[s[i][j]]
def __inv_sub_bytes(self, s):
# 逆字节代换
for i in range(4):
for j in range(4):
s[i][j] = InvSbox[s[i][j]]
def __shift_rows(self, s):
# 行移位
s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]
def __inv_shift_rows(self, s):
# 逆行移位
s[0][1], s[1][1], s[2][1], s[3][1] = s[3][1], s[0][1], s[1][1], s[2][1]
s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
s[0][3], s[1][3], s[2][3], s[3][3] = s[1][3], s[2][3], s[3][3], s[0][3]
def __mix_single_column(self, a):
# 混合单列
t = a[0] ^ a[1] ^ a[2] ^ a[3]
u = a[0]
a[0] ^= t ^ xtime(a[0] ^ a[1])
# a0 ^ (a0 ^ a1 ^ a2 ^ a3) ^ (0x02 * (a0 ^ a1))
# (0x02 * a0) ^ (0x03 * a1) ^ (0x01 * a2) ^ (0x01 * a3)
a[1] ^= t ^ xtime(a[1] ^ a[2])
a[2] ^= t ^ xtime(a[2] ^ a[3])
a[3] ^= t ^ xtime(a[3] ^ u)
# | 02 03 01 01 |
# | 01 02 03 01 |
# | 01 01 02 03 |
# | 03 01 01 02 |
# 0x01 * x = x(不需要计算)
# 0x02 * x = xtime(x)
# 0x03 * x = x ^ xtime(x)
# new_state[0] = (0x02 * state[0]) ^ (0x03 * state[1]) ^ (0x01 * state[2]) ^ (0x01 * state[3])
# new_state[1] = (0x01 * state[0]) ^ (0x02 * state[1]) ^ (0x03 * state[2]) ^ (0x01 * state[3])
# new_state[2] = (0x01 * state[0]) ^ (0x01 * state[1]) ^ (0x02 * state[2]) ^ (0x03 * state[3])
# new_state[3] = (0x03 * state[0]) ^ (0x01 * state[1]) ^ (0x01 * state[2]) ^ (0x02 * state[3])
def __mix_columns(self, s):
# 列混淆
for i in range(4):
self.__mix_single_column(s[i])
def __inv_mix_columns(self, s):
# 逆列混淆
for i in range(4):
# * 0x04
u = xtime(xtime(s[i][0] ^ s[i][2]))
v = xtime(xtime(s[i][1] ^ s[i][3]))
s[i][0] ^= u
s[i][1] ^= v
s[i][2] ^= u
s[i][3] ^= v
self.__mix_columns(s)
# | 0E 0B 0D 09 |
# | 09 0E 0B 0D |
# | 0D 09 0E 0B |
# | 0B 0D 09 0E |
# 0x0E * x = xtime(xtime(xtime(x))) ^ xtime(xtime(x)) ^ xtime(x)
# 0x0B * x = xtime(xtime(xtime(x))) ^ xtime(x) ^ x
# 0x0D * x = xtime(xtime(xtime(x))) ^ xtime(xtime(x)) ^ x
# 0x09 * x = xtime(xtime(xtime(x))) ^ x
# new_state[0] = (0x0E * state[0]) ^ (0x0B * state[1]) ^ (0x0D * state[2]) ^ (0x09 * state[3])
# new_state[1] = (0x09 * state[0]) ^ (0x0E * state[1]) ^ (0x0B * state[2]) ^ (0x0D * state[3])
# new_state[2] = (0x0D * state[0]) ^ (0x09 * state[1]) ^ (0x0E * state[2]) ^ (0x0B * state[3])
# new_state[3] = (0x0B * state[0]) ^ (0x0D * state[1]) ^ (0x09 * state[2]) ^ (0x0E * state[3])
if __name__ == "__main__":
# print("%x" % Sbox[0x00])
passGUI.py
import tkinter as tk
from tkinter import messagebox
from tkinter import ttk
from aes import AES
class AESApp:
def __init__(self, root):
self.root = root
self.root.title("AES 加密/解密工具")
# 创建 Notebook(选项卡)
self.notebook = tk.ttk.Notebook(root)
self.notebook.pack(fill="both", expand=True)
# 创建加/解密选项卡
self.create_encrypt_decrypt_tab()
def create_encrypt_decrypt_tab(self):
# 创建加/解密选项卡
tab = ttk.Frame(self.notebook)
self.notebook.add(tab, text="加/解密")
# 原文输入框
input_label = ttk.Label(tab, text="原文:")
input_label.grid(row=0, column=0, padx=10, pady=10, sticky="w")
self.input_text = tk.Text(tab, height=15, width=80)
self.input_text.grid(row=0, column=1, padx=10, pady=10)
# 密钥输入框
key_label = ttk.Label(tab, text="密钥:")
key_label.grid(row=1, column=0, padx=10, pady=10, sticky="w")
self.key_entry = ttk.Entry(tab, width=80)
self.key_entry.grid(row=1, column=1, padx=10, pady=10, sticky="w")
# 创建一个 Frame 来放置按钮
button_frame = ttk.Frame(tab)
button_frame.grid(row=2, column=0, columnspan=2, padx=10, pady=10)
# 加密按钮
encrypt_button = ttk.Button(button_frame, text="👇加密👇", command=self.encrypt_text)
encrypt_button.pack(side="left", padx=10)
# 解密按钮
decrypt_button = ttk.Button(button_frame, text="👆解密👆", command=self.decrypt_text)
decrypt_button.pack(side="left", padx=10)
# 密文输出框
output_label = ttk.Label(tab, text="密文:")
output_label.grid(row=3, column=0, padx=10, pady=10, sticky="w")
self.output_text = tk.Text(tab, height=15, width=80)
self.output_text.grid(row=3, column=1, padx=10, pady=10)
def encrypt_text(self):
# 获取输入
plaintext = self.input_text.get("1.0", tk.END).strip()
key = self.key_entry.get().strip()
# 检查输入是否为空
if not plaintext or not key:
messagebox.showerror("错误", "请输入原文和密钥!")
return
try:
# 将密钥转换为整数
key_int = int(key, 16)
# 初始化 AES
aes = AES(key_int)
# 计算需要补充的字符数
padding_length = (32 - len(plaintext) % 32) % 32
# 补充字符
s_padded = plaintext + '0' * padding_length
# 分组
groups = [s_padded[i:i+32] for i in range(0, len(s_padded), 32)]
ciphertext_str = ''
for group in groups:
# 加密
ciphertext_str += str(hex(aes.encrypt(int(group, 16))))[2:]
print(group)
# 显示结果到密文框
self.output_text.delete("1.0", tk.END)
self.output_text.insert(tk.END, ciphertext_str)
except ValueError:
messagebox.showerror("错误", "请输入有效的16进制数!")
def decrypt_text(self):
# 获取输入
ciphertext = self.output_text.get("1.0", tk.END).strip()
key = self.key_entry.get().strip()
# 检查输入是否为空
if not ciphertext or not key:
messagebox.showerror("错误", "请输入密文和密钥!")
return
try:
# 将密钥转换为整数
key_int = int(key, 16)
# 初始化 AES
aes = AES(key_int)
# 计算需要补充的字符数
padding_length = (32 - len(ciphertext) % 32) % 32
# 补充字符
s_padded = ciphertext + '0' * padding_length
# 分组
groups = [s_padded[i:i+32] for i in range(0, len(s_padded), 32)]
plaintext_str = ''
for group in groups:
# 解密
plaintext_str += str(hex(aes.decrypt(int(group, 16))))[2:]
print(group)
# 显示结果到原文框
self.input_text.delete("1.0", tk.END)
self.input_text.insert(tk.END, plaintext_str)
except ValueError:
messagebox.showerror("错误", "请输入有效的16进制数!")
if __name__ == "__main__":
root = tk.Tk()
app = AESApp(root)
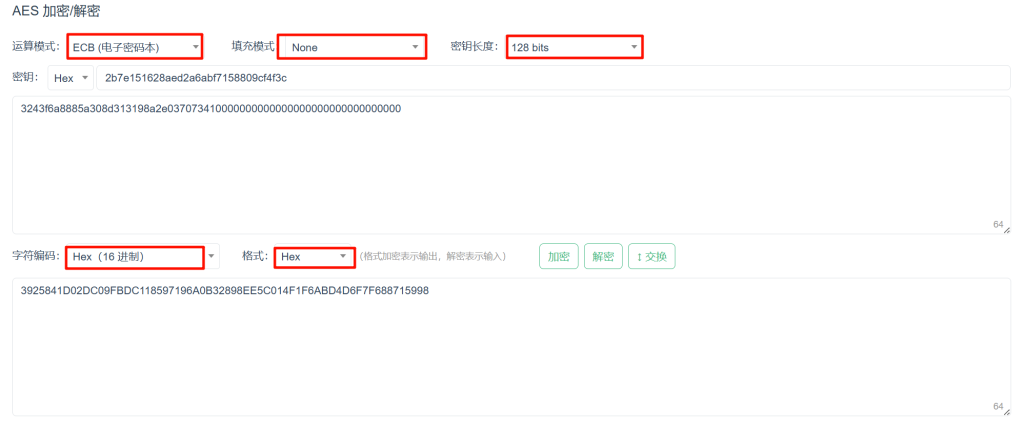
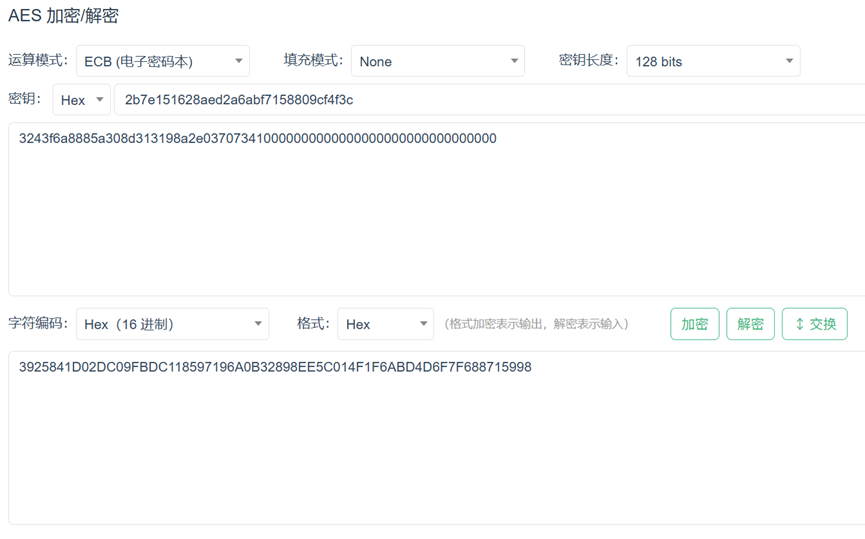
root.mainloop()验证方法
按照如下设置即可验证: