算法主要原理
加密公式:C = (P + K)%26
- C:密文
- P:原文
- K:第几套加密方式
解密公式:P = (C – K)%26
- C:密文
- P:原文
- K:第几套加密方式
- 如果P<0,P+26取得正序
简单来说,Vigenere密码实际上就是分组的凯撒密码。而分组的方法就是重复密钥,密钥相同的明文为同一组。每一组都可以看作是由不同的密钥所加密的凯撒密码。
算法步骤
加/解密
维吉尼亚密码是一种经典的多表替换加密算法,其改进了凯撒密码单表替换的弱点,通过使用不同的字母移位规则,使得频率分析攻击更加困难。
实际上可以将维吉尼亚密码理解为多个凯撒密码的加密,它的核心思想是用一个关键词来控制加密过程,使得同样的字母在明文的不同位置可能会被加密成不同的密文字母,这样就比简单的凯撒密码安全得多。
加密的时候就是把明文的每个字母按照密钥字母对应的数值进行移位,比如密钥字母A代表移0位(相当于不变),B移1位,一直到Z移25位。例如,当加密”HELLO”这个单词,选择的密钥是”KEY”,首先要把密钥重复到和明文一样长变成”KEYKE”,然后每个明文字母都对应一个密钥字母。然后每个字母加密时,H(在字母表里排第7位)对应K(排第10位),就往后移10位变成R(第17位);E(第4位)对应E(第4位),移4位变成I(第8位);第一个L(第11位)对应Y(第24位),11加24等于35,因为字母表只有26个字母,所以35减26得到9,对应J;第二个L(第11位)对应K(第10位),11加10等于21,对应V;O(第14位)对应E(第4位),14加4等于18,对应S。这样最终”HELLO”就被加密成了”RIJVS”。但要注意的是字母表是循环的,超过Z就要回到A继续算,所以计算时要取模26。
解密过程与加密过程相反,用密文字母和密钥字母相减,比如R(17位)减去K(10位)得到7对应H,I(8位)减E(4位)得到4对应E,以此类推。如果遇到字母相减得到负数的情况,把负数加上26就能得到正确的结果。
破解
维吉尼亚密码的核心安全特性来自于它的多表代换机制,但这也恰恰成为它被破解的突破口。要理解破解原理,我们需要先认清一个关键事实:维吉尼亚密码本质上是多个凯撒密码的交替使用。
具体说来则是密钥长度决定了位移序列的长度,也即维吉尼亚密码是在循环应用一组固定的凯撒密码。若是我们确定了其密钥长度,则分组后的密码实际上呈现出单表特性,每组内部都是纯粹的凯撒密码,完全保留自然语言的统计特征。
因此破解维吉尼亚密码的重中之重是要破解出密钥长度,确定了密钥长度后就和破解凯撒密码无异了。所以说我们的破解步骤就分为确定密钥长度和确定密钥内容两步。
(一)确定密钥长度——重合指数法确定密钥长度
确定密钥长度这一步,我们采用重合指数法来确定。
因为对于正常的英语分布来说,从正常英语句子中随机取两个元素相同的概率是0.065,而如果是完全随机的字符串概率则是0.038。0.038~0.065之间的差距,让我们可以检验某一段文字是否符合正常的英语分布。
所以说,我们先假定密钥长度,便可以分出多组密文。每组密文内都是用相同的密钥加密的,因此只要是正常的、有意义的英文句子便符合0.065的概率。我们遍历可能的密钥长度,计算出接近0.065的值后取最小值就可以得到密钥长度。(当遍历的密钥长度稍长时,可能会出现真正密钥长度的倍数的IC会更接近0.065的情况,因此最好选容许的误差范围中的最小值)
以下是详细的数学证明过程:

(二)确定密钥内容——使用卡方检验确定密钥的内容
在确定密钥内容这一步,我们使用卡方检验来确定。
之前的步骤中我们已经将维吉尼亚密码转换为了多组凯撒密码。而对于凯撒密码来说,因为所有自然语言都存在特定的字母出现频率规律,单表替换加密虽然改变了字母的表象,但完整保留了这种统计特征。以英语为例,字母E的出现频率高达12.7%,T约9.1%,A约8.2%,这种分布特征就像语言的”指纹”一样稳定。当我们将明文通过凯撒密码加密时,整个字母表只是被整体平移了一定位数,比如位移3的情况下,原本高频的E会被统一替换成H,T变成W,A变成D,此时密文中H、W、D就会成为新的高频字母,它们与原始高频字母的对应关系完全由位移量决定。
那我们首先需要统计密文中各字母的出现频率,制作频率分布表,然后将这个统计结果与目标语言的标准字母频率进行对比匹配,这一步我们使用卡方检验。卡方检验可以通过量化比较两个字母频率分布的差异程度,来找出最可能使用的位移量。这个卡方值的计算公式是:将每个字母在解密文本中的观察频次与标准英语中的期望频次之差的平方除以期望频次后求和。卡方值越小,说明解密后的字母频率分布与标准英语越接近,也就意味着这个位移量越有可能是正确的密钥。求出密钥后,我们便可以轻松解密维吉尼亚密码了。
总结
破解Vigenere算法最主要就是两个步骤——确定密钥长度和确定密钥内容,而这两个步骤实际上都是利用了英语字母的分布规律来破解的,一个是通过重合指数,一个是通过卡方检验。
程序运行截图
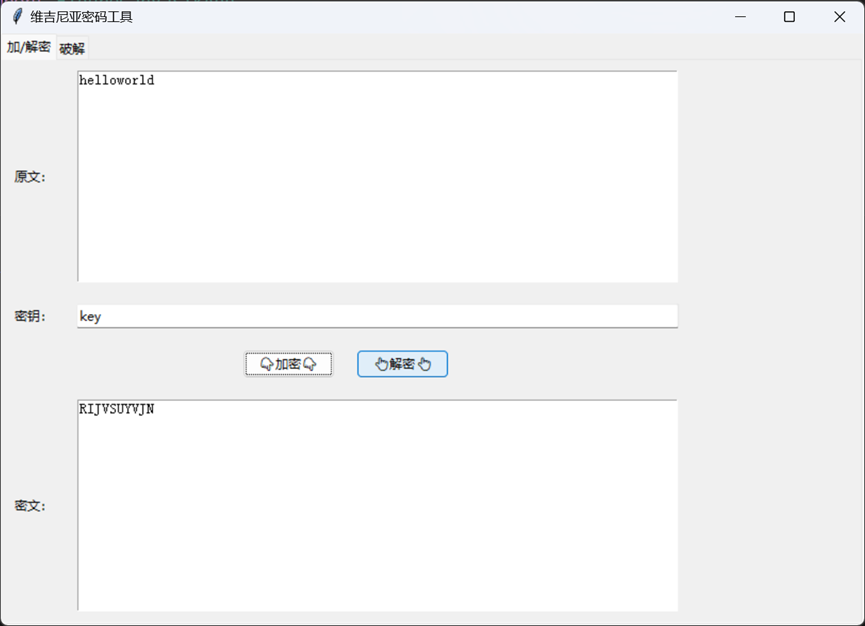
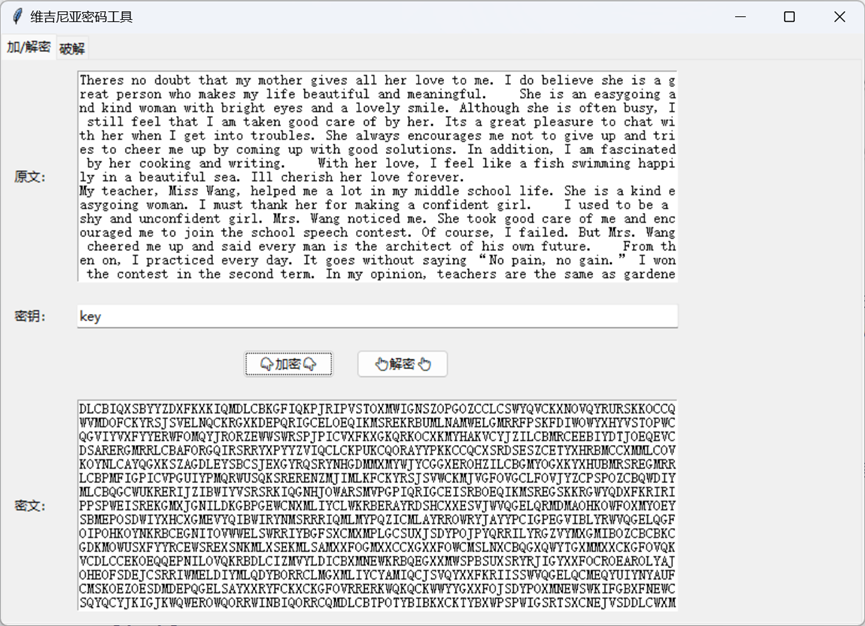
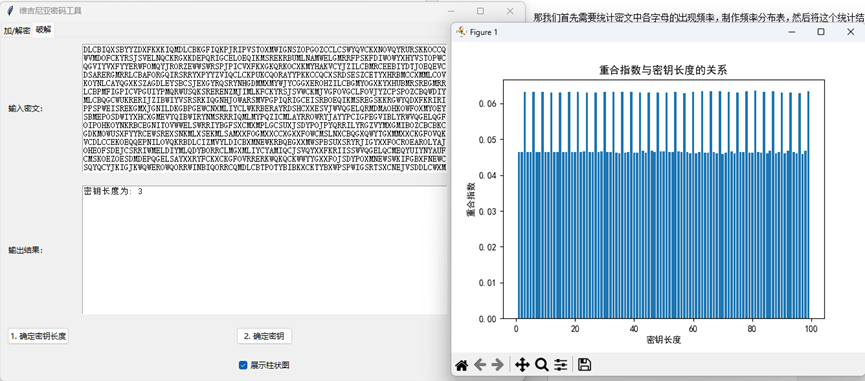
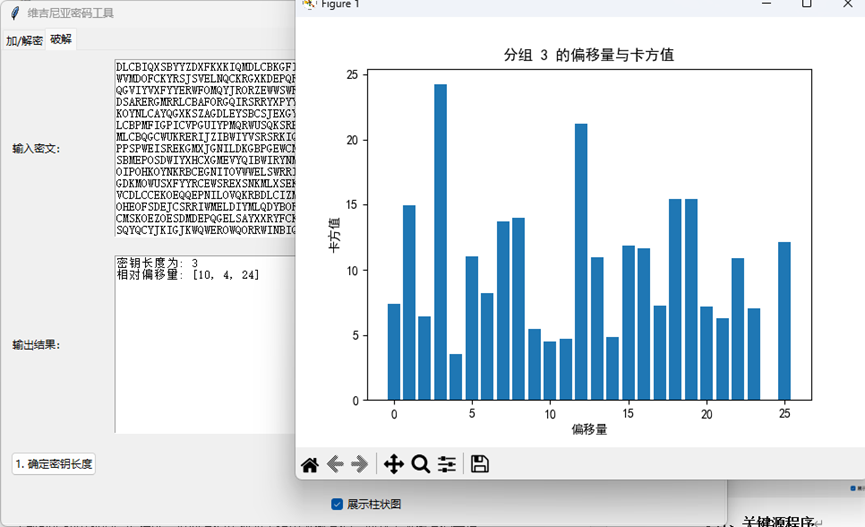
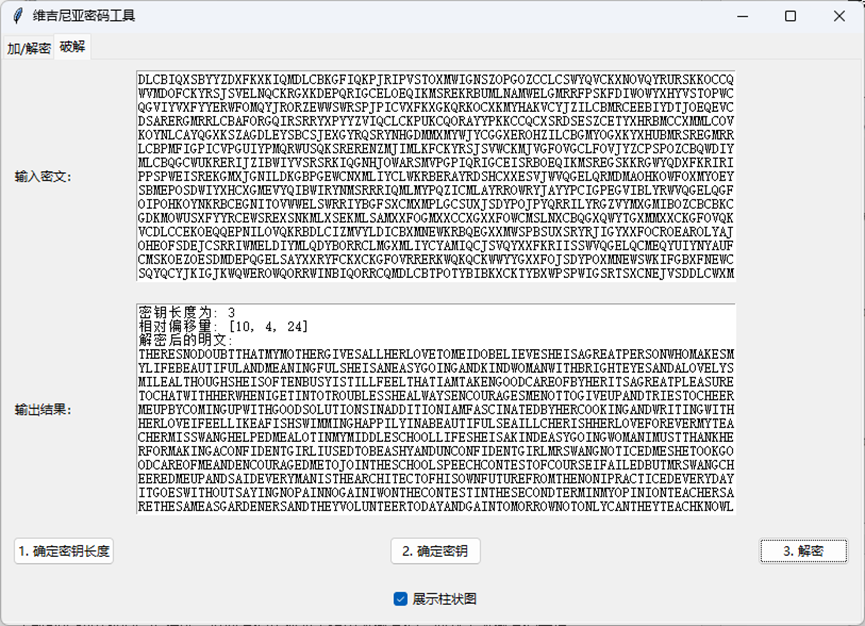
参考代码
endecrypt.py
# Vigenere Cipher Encrypt/Decrypt
# 字母转数字
def L2N(L):
return ord(L.upper()) - ord('A')
# 数字转字母
def N2L(N):
return chr(N + ord('A'))
# 加密
def encrypt(text, key):
encrypted_text = ''
j=0
for i in range(len(text)):
if(text[i].isalpha()):
encrypted_text += N2L((L2N(text[i]) + L2N(key[j%len(key)])) % 26)
j+=1
return encrypted_text
# 解密
def decrypt(text, key):
decrypted_text = ''
j=0
for i in range(len(text)):
decrypted_text += N2L((L2N(text[i]) - L2N(key[j%len(key)])) % 26)
j+=1
return decrypted_text
if __name__ == '__main__':
text = 'I am alive here, my beloved, for the reason to adore you. Oh!How anxious I have been for you and how sorry I am about all you must have suffered in having no news from us. May heaven grant that this letter reaches you. Do not write to me, this would compromise all of us and above all,do not return under any circumstances. It is known that it was you who helped us to get away from here and all would be lost if you should show yourself.We are guarded day and night. I do not care you are not here. Do not be troubled on my account. Nothing will happen to me. The national assemble will show leniency. Farewell the most loved of men. Be quiet if you can take care of yourself.For myself I cannot write any more, but nothing in the world could stop me to adore you up to the death.'
key = 'crypt'
print(encrypt(text, key).lower())crack.py
# Vigenere Cipher Crack
import math
import numpy as np
from typing import List, Tuple
def alpha(cipher: str) -> str:
"""
预处理函数:去掉密文中的非字母字符(如空格、回车、标点符号等)。
:param cipher: 密文字符串
:return: 只包含字母的密文字符串
"""
c = ""
for char in cipher:
if char.isalpha():
c += char
return c
def count_IC(cipher: str) -> float:
"""
计算字符串的重合指数(IC)。
:param cipher: 密文字符串
:return: 重合指数值
"""
count = [0] * 26
L = len(cipher)
IC = 0.0
for char in cipher:
if char.isupper():
count[ord(char) - ord("A")] += 1
elif char.islower():
count[ord(char) - ord("a")] += 1
for i in range(26):
IC += (count[i] * (count[i] - 1)) / (L * (L - 1))
return IC
def count_key_len(cipher: str, key_len: int) -> float:
"""
对密文按密钥长度分组,并计算每组的平均重合指数。
:param cipher: 密文字符串
:param key_len: 密钥长度
:return: 平均重合指数
"""
groups = [""] * key_len
IC = [0] * key_len
for i in range(len(cipher)):
m = i % key_len
groups[m] += cipher[i]
for i in range(key_len):
IC[i] = count_IC(groups[i])
print(f"长度为{key_len}时, 平均重合指数为{np.mean(IC):.5f}")
return np.mean(IC)
def determine_key_length(cipher: str, tolerance: float = 0.01) -> int:
"""
确定最可能的密钥长度。
:param cipher: 密文字符串
:param tolerance: 允许的重合指数误差范围
:return: 最可能的密钥长度
"""
possible_lengths = [] # 存储可能的密钥长度
for key_len in range(1, 100): # 尝试密钥长度从1到100
avg_IC = count_key_len(cipher, key_len)
if abs(avg_IC - 0.065) <= tolerance:
possible_lengths.append((key_len, avg_IC))
if not possible_lengths:
print("未找到符合条件的密钥长度,请调整误差允许范围或检查密文。")
return 0
# 选择误差允许范围内的最短密钥长度
possible_lengths.sort(key=lambda x: x[0]) # 按密钥长度从小到大排序
key_len, avg_IC = possible_lengths[0]
print(f"密钥长度为{key_len}, 此时重合指数每组的平均值为{avg_IC:.5f}")
return key_len
def determine_key_length_old(cipher: str) -> int:
"""
确定最可能的密钥长度。(老旧版本)
:param cipher: 密文字符串
:return: 最可能的密钥长度
"""
key_len = 0
min_diff = 100
avg_IC = 0.0
for i in range(1, 10):
current_IC = count_key_len(cipher, i)
if abs(current_IC - 0.065) < min_diff:
min_diff = abs(current_IC - 0.065)
key_len = i
avg_IC = current_IC
print(f"密钥长度为{key_len}, 此时重合指数每组的平均值为{avg_IC:.5f}")
return key_len
def chi_square(vec: List[str], key: int) -> float:
"""
计算卡方统计量,用于评估解密后的文本是否符合英文字母频率分布。
:param vec: 密文的子串(按密钥长度分组后的某一组)
:param key: 尝试的密钥偏移量
:return: 卡方统计量
"""
freq = [0] * 26 # 统计字母频率
for c in vec:
if c.isalpha():
c = c.lower()
c = chr((ord(c) - ord("a") + (26 - key)) % 26 + ord("a"))
freq[ord(c) - ord("a")] += 1
# 英文字母的期望频率
expected_freq = [
0.08167,
0.01492,
0.02782,
0.04253,
0.12702,
0.02228,
0.02015,
0.06094,
0.06966,
0.00153,
0.00772,
0.04025,
0.02406,
0.06749,
0.07507,
0.01929,
0.00095,
0.05987,
0.06327,
0.09056,
0.02758,
0.00978,
0.02360,
0.00150,
0.01974,
0.00074,
]
# 确保期望频率的总和为1.0
assert abs(1.0 - sum(expected_freq)) < 1e-4
n = len(vec) # 子串的长度
chi_square_value = 0.0
for i in range(26):
observed_freq = freq[i] / n # 观察到的频率
chi_square_value += (observed_freq - expected_freq[i]) ** 2 / expected_freq[i]
return chi_square_value
def determine_relative_shifts(cipher: str, key_len: int) -> List[int]:
"""
使用卡方检验确定每组最可能的相对偏移量。
:param cipher: 密文字符串
:param key_len: 密钥长度
:return: 相对偏移量列表
"""
possible_key = [] # 存储可能的密钥
for i in range(key_len):
# 生成当前分组的子串
vec = [cipher[j] for j in range(i, len(cipher), key_len)]
# 尝试所有可能的偏移量(0-25)
possibility_array = []
for j in range(26):
curr_chi_square = chi_square(vec, j)
possibility_array.append((chr(ord("a") + j), curr_chi_square))
# 按卡方值从小到大排序(卡方值越小,可能性越大)
possibility_array.sort(key=lambda x: x[1])
# 选择卡方值最小的偏移量作为当前分组的密钥字母
possible_key.append(ord(possibility_array[0][0]) - ord("a"))
return possible_key
def decrypt(cipher: str, key_len: int, shifts: List[int]) -> str:
"""
使用密钥对密文进行解密。
:param cipher: 密文字符串
:param key_len: 密钥长度
:param shifts: 密钥字母的下标列表
:return: 解密后的明文字符串
"""
plain = ""
i = 0
while i < len(cipher):
for j in range(key_len):
if cipher[i].isupper():
plain += chr(
(ord(cipher[i]) - ord("A") - shifts[j] + 26) % 26 + ord("A")
)
else:
plain += chr(
(ord(cipher[i]) - ord("a") - shifts[j] + 26) % 26 + ord("a")
)
i += 1
if i == len(cipher):
break
return plain
if __name__ == "__main__":
cipher = alpha(input("输入密文:"))
# 第一步:确定密钥长度
key_len = determine_key_length(cipher)
# 第二步:使用卡方检验确定密钥
shifts = determine_relative_shifts(cipher, key_len)
print("相对偏移量:", shifts)
# 第三步:解密
plain = decrypt(cipher, key_len, shifts)
print("解密后的明文:", plain)
GUI.py
import math
import numpy as np
from typing import List, Tuple
import tkinter as tk
from tkinter import ttk, messagebox
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
import matplotlib.pyplot as plt
# Set the font family to SimHei (黑体)
plt.rcParams['font.family'] = 'SimHei'
# 字母转数字
def L2N(L):
return ord(L.upper()) - ord('A')
# 数字转字母
def N2L(N):
return chr(N + ord('A'))
# 加密
def encrypt(text, key):
encrypted_text = ''
j = 0
for i in range(len(text)):
if text[i].isalpha():
encrypted_text += N2L((L2N(text[i]) + L2N(key[j % len(key)])) % 26)
j += 1
return encrypted_text
# 解密
def decrypt_vigenere(text, key):
decrypted_text = ''
j = 0
for i in range(len(text)):
if text[i].isalpha():
decrypted_text += N2L((L2N(text[i]) - L2N(key[j % len(key)])) % 26)
j += 1
return decrypted_text
# 核心函数
def alpha(cipher: str) -> str:
"""
预处理函数:去掉密文中的非字母字符(如空格、回车、标点符号等)。
:param cipher: 密文字符串
:return: 只包含字母的密文字符串
"""
c = ""
for char in cipher:
if char.isalpha():
c += char
return c
def count_IC(cipher: str) -> float:
"""
计算字符串的重合指数(IC)。
:param cipher: 密文字符串
:return: 重合指数值
"""
count = [0] * 26
L = len(cipher)
IC = 0.0
for char in cipher:
if char.isupper():
count[ord(char) - ord("A")] += 1
elif char.islower():
count[ord(char) - ord("a")] += 1
for i in range(26):
IC += (count[i] * (count[i] - 1)) / (L * (L - 1))
return IC
def count_key_len(cipher: str, key_len: int) -> float:
"""
对密文按密钥长度分组,并计算每组的平均重合指数。
:param cipher: 密文字符串
:param key_len: 密钥长度
:return: 平均重合指数
"""
groups = [""] * key_len
IC = [0] * key_len
for i in range(len(cipher)):
m = i % key_len
groups[m] += cipher[i]
for i in range(key_len):
IC[i] = count_IC(groups[i])
return np.mean(IC)
def determine_key_length(cipher: str, tolerance: float = 0.01) -> int:
"""
确定最可能的密钥长度。
:param cipher: 密文字符串
:param tolerance: 允许的重合指数误差范围
:return: 最可能的密钥长度
"""
possible_lengths = [] # 存储可能的密钥长度
IC_values = [] # 存储每个密钥长度对应的重合指数
for key_len in range(1, 100): # 尝试密钥长度从1到100
avg_IC = count_key_len(cipher, key_len)
IC_values.append(avg_IC)
if abs(avg_IC - 0.065) <= tolerance:
possible_lengths.append((key_len, avg_IC))
if not possible_lengths:
raise ValueError("未找到符合条件的密钥长度,请调整误差允许范围或检查密文。")
# 选择误差允许范围内的最短密钥长度
possible_lengths.sort(key=lambda x: x[0]) # 按密钥长度从小到大排序
key_len, avg_IC = possible_lengths[0]
return key_len, IC_values
def chi_square(vec: List[str], key: int) -> float:
"""
计算卡方统计量,用于评估解密后的文本是否符合英文字母频率分布。
:param vec: 密文的子串(按密钥长度分组后的某一组)
:param key: 尝试的密钥偏移量
:return: 卡方统计量
"""
freq = [0] * 26 # 统计字母频率
for c in vec:
if c.isalpha():
c = c.lower()
c = chr((ord(c) - ord('a') + (26 - key)) % 26 + ord('a'))
freq[ord(c) - ord('a')] += 1
# 英文字母的期望频率
expected_freq = [
0.08167, 0.01492, 0.02782, 0.04253, 0.12702, 0.02228, 0.02015, 0.06094, 0.06966, 0.00153,
0.00772, 0.04025, 0.02406, 0.06749, 0.07507, 0.01929, 0.00095, 0.05987, 0.06327, 0.09056,
0.02758, 0.00978, 0.02360, 0.00150, 0.01974, 0.00074
]
# 确保期望频率的总和为1.0
assert abs(1.0 - sum(expected_freq)) < 1e-4
n = len(vec) # 子串的长度
chi_square_value = 0.0
for i in range(26):
observed_freq = freq[i] / n # 观察到的频率
chi_square_value += (observed_freq - expected_freq[i]) ** 2 / expected_freq[i]
return chi_square_value
def determine_relative_shifts(cipher: str, key_len: int) -> Tuple[List[int], List[List[float]]]:
"""
使用卡方检验确定每组与第一组之间的相对偏移量。
:param cipher: 密文字符串
:param key_len: 密钥长度
:return: 相对偏移量列表和每一组的卡方值列表(未排序)
"""
possible_key = [] # 存储可能的密钥
chi_square_values = [] # 存储每一组的卡方值(未排序)
for i in range(key_len):
# 生成当前分组的子串
vec = [cipher[j] for j in range(i, len(cipher), key_len)]
# 尝试所有可能的偏移量(0-25)
chi_values = [] # 存储当前分组的卡方值(未排序)
for j in range(26):
curr_chi_square = chi_square(vec, j)
chi_values.append(curr_chi_square)
# 按卡方值从小到大排序(卡方值越小,可能性越大)
sorted_indices = np.argsort(chi_values) # 获取排序后的索引
best_shift = sorted_indices[0] # 选择卡方值最小的偏移量
# 存储结果
possible_key.append(best_shift)
chi_square_values.append(chi_values) # 存储未排序的卡方值
return possible_key, chi_square_values
def decrypt(cipher: str, key_len: int, shifts: List[int]) -> str:
"""
使用密钥对密文进行解密。
:param cipher: 密文字符串
:param key_len: 密钥长度
:param shifts: 密钥字母的下标列表
:return: 解密后的明文字符串
"""
plain = ""
i = 0
while i < len(cipher):
for j in range(key_len):
if cipher[i].isupper():
plain += chr(
(ord(cipher[i]) - ord("A") - shifts[j] + 26) % 26 + ord("A")
)
else:
plain += chr(
(ord(cipher[i]) - ord("a") - shifts[j] + 26) % 26 + ord("a")
)
i += 1
if i == len(cipher):
break
return plain
# GUI 界面
class VigenereCrackerApp:
def __init__(self, root):
self.root = root
self.root.title("维吉尼亚密码工具")
self.cipher = ""
self.key_len = 0
self.shifts = []
self.plain = ""
self.show_plots = tk.BooleanVar(value=True) # 是否展示柱状图
# 创建选项卡
self.notebook = ttk.Notebook(root)
self.notebook.pack(fill="both", expand=True)
# 添加“加/解密”选项卡
self.add_encrypt_decrypt_tab()
# 添加“破解”选项卡
self.add_crack_tab()
def add_encrypt_decrypt_tab(self):
"""添加加/解密选项卡"""
tab = ttk.Frame(self.notebook)
self.notebook.add(tab, text="加/解密")
# 输入框
input_label = ttk.Label(tab, text="原文:")
input_label.grid(row=0, column=0, padx=10, pady=10, sticky="w")
self.input_text_encrypt = tk.Text(tab, height=15, width=80)
self.input_text_encrypt.grid(row=0, column=1, padx=10, pady=10)
# 密钥输入框
key_label = ttk.Label(tab, text="密钥:")
key_label.grid(row=1, column=0, padx=10, pady=10, sticky="w")
self.key_entry = ttk.Entry(tab, width=80)
self.key_entry.grid(row=1, column=1, padx=10, pady=10, sticky="w")
# 创建一个 Frame 来放置按钮
button_frame = ttk.Frame(tab)
button_frame.grid(row=2, column=0, columnspan=2, padx=10, pady=10)
# 加密按钮
encrypt_button = ttk.Button(button_frame, text="👇加密👇", command=self.encrypt_text)
encrypt_button.pack(side="left", padx=10)
# 解密按钮
decrypt_button = ttk.Button(button_frame, text="👆解密👆", command=self.decrypt_text)
decrypt_button.pack(side="left", padx=10)
# 输出框
output_label = ttk.Label(tab, text="密文:")
output_label.grid(row=3, column=0, padx=10, pady=10, sticky="w")
self.output_text_encrypt = tk.Text(tab, height=15, width=80)
self.output_text_encrypt.grid(row=3, column=1, padx=10, pady=10)
def add_crack_tab(self):
"""添加破解选项卡"""
tab = ttk.Frame(self.notebook)
self.notebook.add(tab, text="破解")
# 输入框
input_label = ttk.Label(tab, text="输入密文:")
input_label.grid(row=0, column=0, padx=10, pady=10, sticky="w")
self.input_text = tk.Text(tab, height=15, width=80)
self.input_text.grid(row=0, column=1, padx=10, pady=10)
# 输出框
output_label = ttk.Label(tab, text="输出结果:")
output_label.grid(row=1, column=0, padx=10, pady=10, sticky="w")
self.output_text = tk.Text(tab, height=15, width=80)
self.output_text.grid(row=1, column=1, padx=10, pady=10)
# 按钮
self.step1_button = ttk.Button(tab, text="1. 确定密钥长度", command=self.step1)
self.step1_button.grid(row=2, column=0, padx=10, pady=10)
self.step2_button = ttk.Button(tab, text="2. 确定密钥", command=self.step2)
self.step2_button.grid(row=2, column=1, padx=10, pady=10)
self.step3_button = ttk.Button(tab, text="3. 解密", command=self.step3)
self.step3_button.grid(row=2, column=2, padx=10, pady=10)
# 是否展示柱状图
self.plot_check = ttk.Checkbutton(tab, text="展示柱状图", variable=self.show_plots)
self.plot_check.grid(row=3, column=1, padx=10, pady=10)
def encrypt_text(self):
"""加密文本"""
text = self.input_text_encrypt.get("1.0", tk.END).strip() # 获取明文
key = self.key_entry.get().strip() # 获取密钥
if not text or not key:
messagebox.showerror("错误", "请输入明文和密钥!")
return
encrypted_text = encrypt(text, key) # 调用加密函数
self.output_text_encrypt.delete("1.0", tk.END) # 清空输出框
self.output_text_encrypt.insert(tk.END, encrypted_text) # 显示密文
def decrypt_text(self):
"""解密文本"""
text = self.output_text_encrypt.get("1.0", tk.END).strip() # 获取密文
key = self.key_entry.get().strip() # 获取密钥
if not text or not key:
messagebox.showerror("错误", "请输入密文和密钥!")
return
decrypted_text = decrypt_vigenere(text, key) # 调用解密函数
self.input_text_encrypt.delete("1.0", tk.END) # 清空输入框
self.input_text_encrypt.insert(tk.END, decrypted_text) # 显示明文
def step1(self):
"""第一步:确定密钥长度"""
self.cipher = alpha(self.input_text.get("1.0", tk.END).strip())
try:
self.key_len, IC_values = determine_key_length(self.cipher)
self.output_text.delete("1.0", tk.END)
self.output_text.insert(tk.END, f"密钥长度为: {self.key_len}\n")
# 展示重合指数与密钥长度的图
if self.show_plots.get():
self.plot_IC_vs_keylen(IC_values)
except ValueError as e:
messagebox.showerror("错误", str(e))
def step2(self):
"""第二步:确定密钥"""
if not self.key_len:
messagebox.showerror("错误", "请先确定密钥长度!")
return
# 调用 determine_relative_shifts 获取密钥和卡方值
self.shifts, chi_square_values = determine_relative_shifts(self.cipher, self.key_len)
self.output_text.insert(tk.END, f"相对偏移量: {self.shifts}\n")
# 展示每一组的卡方与偏移量的图
if self.show_plots.get():
self.plot_chi_square_vs_shift(chi_square_values)
def step3(self):
"""第三步:解密"""
if not self.shifts:
messagebox.showerror("错误", "请先确定密钥!")
return
self.plain = decrypt(self.cipher, self.key_len, self.shifts)
self.output_text.insert(tk.END, f"解密后的明文: \n{self.plain}\n")
def plot_IC_vs_keylen(self, IC_values):
"""绘制重合指数与密钥长度的柱状图"""
fig, ax = plt.subplots()
x = range(1, len(IC_values) + 1) # 横轴:密钥长度
ax.bar(x, IC_values) # 绘制柱状图
ax.set_xlabel("密钥长度")
ax.set_ylabel("重合指数")
ax.set_title("重合指数与密钥长度的关系")
plt.show()
def plot_chi_square_vs_shift(self, chi_square_values):
"""
绘制每一组的卡方与偏移量的图。
:param chi_square_values: 每一组的卡方值列表(未排序)
"""
for i, chi_values in enumerate(chi_square_values):
fig, ax = plt.subplots()
x = range(26) # 横轴:偏移量(0-25)
ax.bar(x, chi_values) # 绘制柱状图
ax.set_xlabel("偏移量")
ax.set_ylabel("卡方值")
ax.set_title(f"分组 {i+1} 的偏移量与卡方值")
plt.show()
# 运行 GUI
if __name__ == "__main__":
root = tk.Tk()
app = VigenereCrackerApp(root)
root.mainloop()